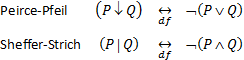Mein Proseminar zur Formalen Logik findet in der Woche vom 21.02.11 – 25.02.11 täglich von 09:00 – 18:00 Uhr in Raum IG 0.457 am Campus Westend der Universität Frankfurt statt. Es ist keine Voranmeldung erforderlich. Die Klausur wird voraussichtlich am 28.02.11 um 17:00 Uhr geschrieben. Empfohlene Literatur: Richard C. Jeffrey (& George Boolos), Formal Logic. Its Scope and Limits, 3rd Edition, New York, Cambridge 1990/2004, oder 4th Edition (by John P. Burgess) 2006.
Proseminar: »Logik«
01.03.10 — Peter GoldMein Proseminar zur »Logik« im Sommersemester 2010 findet als Blockveranstaltung vom 15.03.10 – 19.03.10 von 09:00 – 18:00 Uhr in Raum IG 0.454 am Campus Westend der Universität Frankfurt statt.
Wittgensteins N-Operator im »Tractatus«
31.05.09 — Peter GoldIn Wittgensteins »Tractatus logico-philosophicus« wird ein logischer Operator eingeführt, um die allgemeine Satzstruktur (in formallogischer Hinsicht) zu klären: der N-Operator. Es handelt sich um einen Operator, dessen Operanden (Aussage-) Sätze sind, Propositionen genannt, die einen von zwei Wahrheitswerten annehmen. Der Operator stellt eine Wahrheitsfunktion dar, das heißt eine Funktion (im mathematischen Sinne), welche in Abhängigkeit von den jeweiligen Wahrheitswerten ihrer Argumente ebenfalls Wahrheitswerte als Funktionswerte liefert. Aber anders als übliche Funktionen mit fester Stellenzahl ist der N-Operator für eine beliebige Stellenzahl erklärt. Er wirkt nämlich als monadischer, als dyadischer, als triadischer etc. Operator, je nachdem welche Anzahl von Operanden auftritt, fungiert also für n Operanden als n-adischer oder n-stelliger Operator. Aus technischer Sicht der digitalen Schaltalgebra liegt der Typus des NOR-Gatters (NOR gate) mit variabler Anzahl von Anschlüssen für den Input vor, wobei mit NOR gemeint ist, daß die (kombinierte) Operation »not-or« ausgeführt wird. Der Output eines ähnlichen Schaltkreises, des NAND-Gatters (NAND gate), wird erzeugt, indem der anstehende Input gemäß der Operation »not-and« umgewandelt und anschließend ausgegeben wird, wobei beide Gatter die Negation »not« erst nach der logischen Verknüpfung der Eingangssignale gemäß der Disjunktion »or« beziehungsweise der Konjunktion »and« vornehmen. Wollte man digitale logische Schaltungen auf einen einzigen Typus von vorgefertigen Schaltkreisen reduzieren, wäre jeder der beiden logischen Bausteine geeignet, sämtliche anderen Typen zu ersetzen. In der formalen Logik läßt sich für den Fall von zwei Operanden die Wirkung des NOR-Gatters durch den Peirce-Pfeil symbolisieren, während dem NAND-Gatter das Symbol des Sheffer-Strichs entspricht. Beide werden definiert als:
Die genannten Operatoren sind dual zueinander. Sie waren Peirce (um 1880) beide bekannt, und er wußte auch was von Sheffer (1913) bewiesen wurde, daß nämlich die logischen Operationen in der Boolschen Algebra auf einen von beiden zurückführbar sind. Im »Tractatus« (1921) knüpft Wittgenstein an Sheffer an, Peirce hatte seine eigenen Ergebnisse nicht veröffentlicht, doch benannt ist der betreffende Operator inzwischen nach Peirce, nicht nach Sheffer.
In Form des N-Operators wird der Peirce-Pfeil verallgemeinert, indem keine bestimmte Anzahl von Operanden in dessen Definition angegeben wird: Es werde als Resultat der Operation der Wahrheitswert »falsch« geliefert, wenn und nur wenn mindestens einer der Operanden den Wert »wahr« annimmt, andernfalls sei das Resultat »wahr«. Dies charakterisiert den N-Operator in seiner Wirkung, ohne seine Anwendung an irgendeine feste Stellenzahl zu koppeln. Insofern egeben sich folgende logische Äquivalenzen:
Anhand des N-Operators lassen sich sämtliche logischen Junktoren einführen oder nachbilden, ob einstellig oder mehrstellig, wie Negator, Konjunktor, Disjunktor oder Adjunktor, Konditional, Bikonditional oder Äquivalenz etc. Unter einer Junktorenbasis ist eine Auswahl von Junktoren zu verstehen, mittels derer sämtliche anderen Junktoren definierbar sind. Solche Mengen von Junktoren werden als funktional vollständig bezeichnet. Beispielsweise bilden die beiden Junktoren der Negation und des Konditionals (materiale Implikation) eine Junktorenbasis, ebenso die Negation gemeinsam mit der Konjunktion oder der Disjunktion. Eine Junktorenbasis bildet auch der Peirce-Pfeil allein, ebenso der Sheffer-Strich allein. Wie sich der N-Operator dazu eignet, andere Junktoren zu definieren oder zu emulieren, zeigt sich an folgenden Entsprechungen:

Auf ähnliche Weise sind sämtliche weiteren n-adischen Operatoren der Junktorenlogik definierbar. Dasselbe ist mittels des Peirce-Pfeils oder des dazu dualen Sheffer-Strichs erreichbar, allerdings weisen beide eine feste Stellenzahl auf, was bei Wittgensteins N-Operator eben vermieden wird. Weniger elegant, doch nicht weniger allgemein wäre es, statt Wittgensteins N-Operator einen jener beiden zueinander dualen Operatoren zu wählen. Übrigens gehört zu Wittgensteins N-Operator ebenfalls ein dualer, der als solcher den Sheffer-Strich anstelle des Peirce-Pfeils verallgemeinert. In der Schaltalgebra entspricht, wie gesagt, dem Peirce-Pfeil ein NOR-Gatter und dem Sheffer-Strich ein NAND-Gatter, jeweils mit zwei Eingängen. Werden die beiden Eingänge leitend miteinander verbunden, das heißt kurzgeschlossen, so wirkt sowohl das NOR als auch das NAND-Gatter wie ein Inverter, welcher die Negation des digitalen Eingangssignals liefert, denn es gelten die Äquivalenzen:
In den angegebenen Formeln zeichnet sich ab, inwiefern im Rekurs auf den N-Operator von Wttgenstein die beabsichtigte strukturelle Vereinheitlichung verschachtelter Junktoren erzielbar ist, um die formale Diversität logischer Operatoren auf einen einzigen Operationstyp zu reduzieren. Wenn die Bedeutung eines Satzes nicht von oberflächlichen Umformungen beinflußt wird, sondern allein von dessen Wahrheitsbedingungen abhängt, wobei letztere in logischen Operatoren codiert sind, dient es der formalen Einheitlichkeit und Durchsichtigkeit, wenn auch nicht der Bequemlichkeit, eine einzige logische Operation als fundamental auszuzeichnen und andere Operationen dadurch auszudrücken. Ohne eine gewisse Konvergenz der komplexen Formen gleichbedeutender Propositionen ergäbe sich kein Anhaltspunkt, an dem so etwas wie eine allgemeine Satzform festzumachen wäre.
(Copyright by Peter Gold)
Seminar: »Formale Logik«
06.03.09 — Peter GoldMein Seminar zur Einführung in die »Formale Logik« im Sommersemester 2009 findet vom 16.03.09 bis 20.03.09 um 09:00-18:00 Uhr am Campus Westend im Hörsaal IG 457 der Universität Frankfurt statt. Behandelt wird die Junktoren- und Quantoren-Logik. Es ist keine Voranmeldung zur Teilnahme an der Lehrveranstaltung erforderlich. Den Abschluß des Blockseminars bildet eine Klausur, die voraussichtlich nachmittags am 23.03.09 geschrieben wird.